研究事例

先端的確率統計学が開く大規模従属性モデリング
研究者名 吉田 朋広 研究者所属 東京大学大学院数理科学研究科教授キーワード 従属性、確率過程、統計推測、確率解析、統計的学習理論、超高頻度データ、YUIMA
研究内容
A:どんな諸分野・企業の、どんな問題や現象をターゲットにしたか。
今日、計測とストレージ技術の発展によって、超高頻度ビッグデータが利用可能になっている。データは強従属、高次元、非線形、非エルゴード的となり、現象のモデリングと予測を可能するための確率過程の統計学の構築は、時系列データが現れる諸科学の発展に関わる普遍的な課題である。
B:どんな数学・数理科学をどのように使ったか。
数理統計学(漸近決定理論、確率場の収束理論、ベイズ統計、情報量規準、ノンパラメトリック統計)、確率論(極限定理、漸近展開、セミマルチンゲール理論、マリアバン解析、レビ過程、フラクショナルブラウン運動)、統計的学習理論(スパース推定、正則化法)、計算機統計学(MCMC、最適化)が使われているが、関数解析、微分方程式論、微分幾何、計算機科学など確率統計学以外の分野も広く関わっている。自ら構築した擬似尤度解析・非同期共分散推定・漸近展開の理論は重要な役割を果たしている。
C:どんな成果が得られたか。(あるいは、どんな成果を目指しているか。)
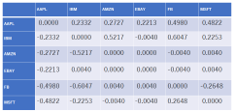
リミットオーダーブックのモデリング、時系列間の因果律を発見するリードラグ解析法、擬似尤度解析による従属モデルでのベイズ推定量の漸近挙動の解明、高速なMCMCアルゴリズムの開発、確率微分方程式のマルチステップハイブリッド推定量の提案、LASSOなどの正則化法の従属モデルにおける挙動の解明、QBICなどの情報量規準、無限次元確率解析によるウイナー汎関数の漸近展開理論などの成果を得ている。また、Rパッケージ YUIMA および yuimaGUI として、非専門家も容易に最新の結果が利用できるようになっている。
D:どのようなきっかけでその諸分野・企業との連携が始まったか。
金融高頻度データ解析はもとより確率過程の統計学の応用分野であったので連携は自然に始まった。また、我々が提唱したオプション価格の漸近展開による近似法や非同期共分散推定法は広く使われており、金融ソリューション企業との共同研究もある。
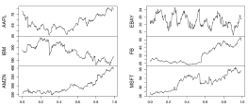 リードラグの発見
リードラグの発見