2017K004 研究テーマ

美的要素を内在した幾何学的形状生成の理論とその実装

研究者名 梶原健司 研究者所属 九州大学マス・フォア・インダストリ研究所
キーワード 対数型美的曲線，微分幾何，可積分系，意匠設計，離散微分幾何，相似幾何，クライン幾何，特殊関

---

研究内容

A：どんな諸分野・企業の、どんな問題や現象をターゲットにしたか。

工業意匠設計（自動車のデザインなど）の設計で美しい形状を効率的に設計するために，美的要素を内在した形状要素として開発された平面曲線の族「対数型美的曲線」の数学的枠組みの構築とその空間曲線や曲面への一般化．また，その高品質かつ高速な実装．

B：どんな数学・数理科学をどのように使ったか。

曲線・曲面の微分幾何学，特に，幾何形状への群作用とそれに対する不変性に着目するクライン幾何学．そのうち「相似幾何」と呼ばれるクライン幾何学と，その枠組みでの曲線の可積分変形理論，またその可積分離散化

C：どんな成果が得られたか。(あるいは、どんな成果を目指しているか。)

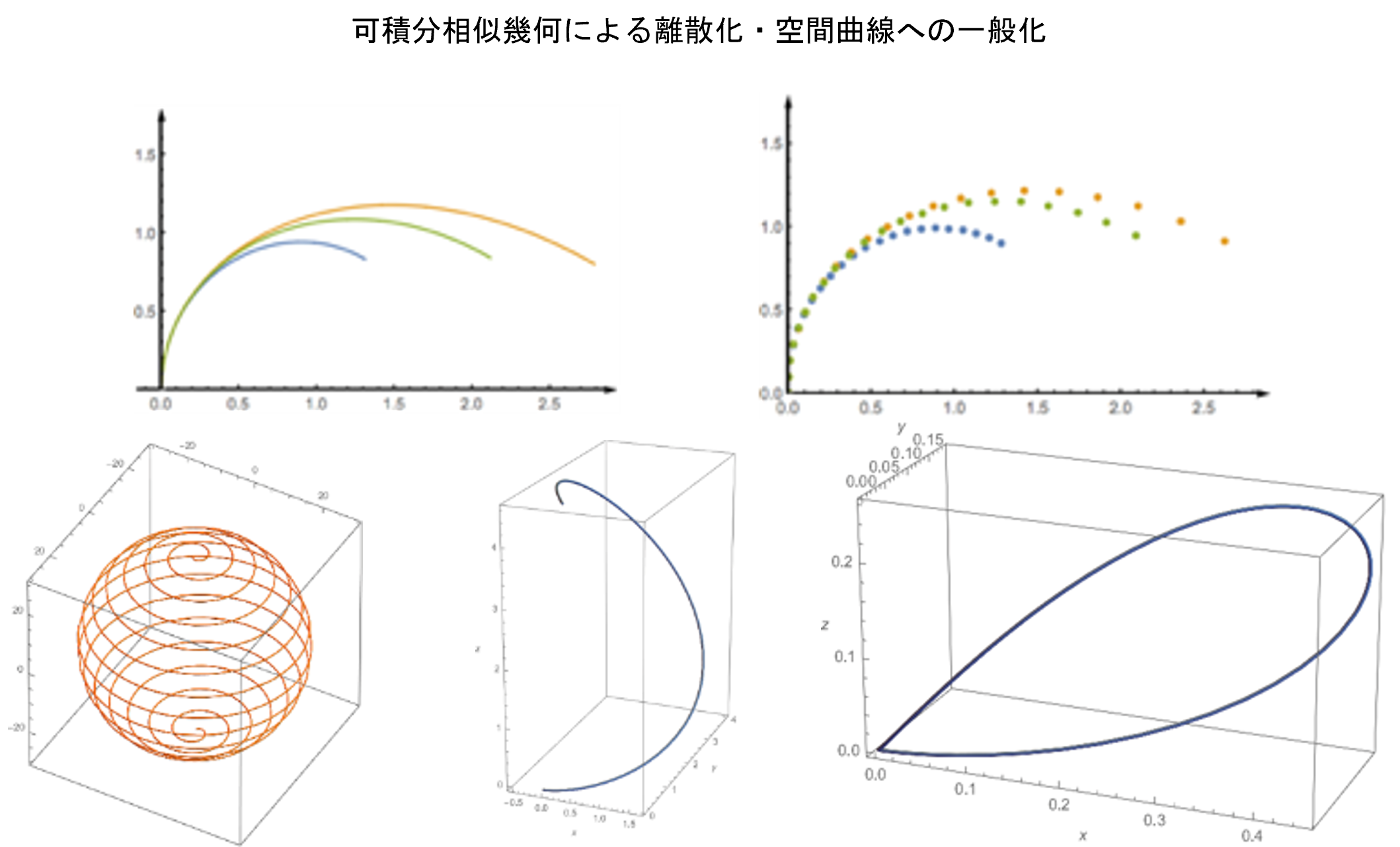
通常のユークリッド幾何の枠組みで研究されていた対数型美的曲線を相似幾何の枠組みを適用して定式化し，それらが相似平面曲線の可積分剛体変形として理解でき，変分原理で定式化できることを示した．すなわち対数型美的曲線が，弾性工学などで基本モデルとして著名なユークリッド幾何におけるオイラーの弾性曲線の相似幾何類似である．この理論的枠組みを基盤として，高品質かつ高速な離散化と実装，および空間曲線への拡張を得た．現在，「美的曲面」の理論を構築中で，さらに，建築や造船の専門家との協働で，「望ましい」形状を可積分（離散）クライン幾何の枠組みで生成する研究プロジェクトを準備中である．

D：どのようなきっかけでその諸分野・企業との連携が始まったか。

企業におけるCADの技術者から対数型美的曲線の数学的枠組みについて相談を受け，公募制のIMI短期研究員制度を利用してその研究者と共同研究を始め，次年度にIMI短期共同研究計画を企画して採択された．

---